Title: Dynamic Knowledge Graph Construction for Zero-shot Commonsense Question Answering
Authors: Antoine Bosselut, Yejin Choi
Org.: AI2
Published: null
Motivation
理解叙事体裁的文本 (narratives) 需要对文本中描述情境 (situation) 的隐式因果 (causal and effect) 、状态 (state) 进行动态推理。
而仅根据文本中明确说明的信息只能得到平凡的情境细节。
以 “they went to the club” 这句 statement 为例,其背后还蕴含了相关的常识信息 (commonsense expectations),如:
- they had to get dressed;
- they were going dancing;
- they likely had drinks;
这其中涉及到/需要关于社会 (social) 和物理 (physical) 世界的丰富背景知识。
相关工作侧重于:利用从大规模知识库中检索得到的知识来增强神经网络模型;
- 这些工作的前提是: 可以通过实体链接,联结文本和 KB ;
- 但是,通过规范化输入中的实体,会丢失输入中的关键上下文,导致抽取得到的是语义无关知识;
面临的核心挑战是:如何按需访问上下文相关的知识并对其进行推理。
This Work
本文针对 zero-shot commonsense QA 进行研究,将该任务转化为:在动态产生的知识图上进行概率推理;
- 与之前的工作 (从静态KB中检索已存在的知识进行知识整合) 不同,本文侧重于:上下文相关的知识可能不存在于现有的KB中;
- 提出了一种,使用生成式神经常识知识模型 (COMET) 按需生成上下文相关知识的方法。
- 本文方法的重点:生成知识 -> 构建知识图
- 本文方法的优势:不需要规范实体来连接到一个静态的知识图谱,知识模型可以直接用于查询知识 (生成需要的知识)
实验数据集:
- socialIQA
- story commonsense
补充:本文是在 COMET[1] 工作的基础之上展开的,也可以看做是 COMET 在 Commonsense QA 领域的应用。
Method: Dynamic Construction of Intermediate Knowledge Graphs
给定一个 raw context,COMET 生成常识推理 (即,生成与context中描述情境相关的世界知识) ,此推理作为额外的 context 用于 a) 给候选答案打分;b) 生成更多的常识推理。
COMET 生成的常识推理,连接 raw context 和候选答案,从而动态的构建起一个 KG :
- raw context 为 KG 的 root 节点;
- 候选答案为 leaf 节点;
- 生成的常识推理为推理路径;
- 可以用COMET生成常识推理的打分作为路径/边的权重;
最后,基于这个动态构建的 KG 进行概率推理,确定最终的答案。
整体的流程图: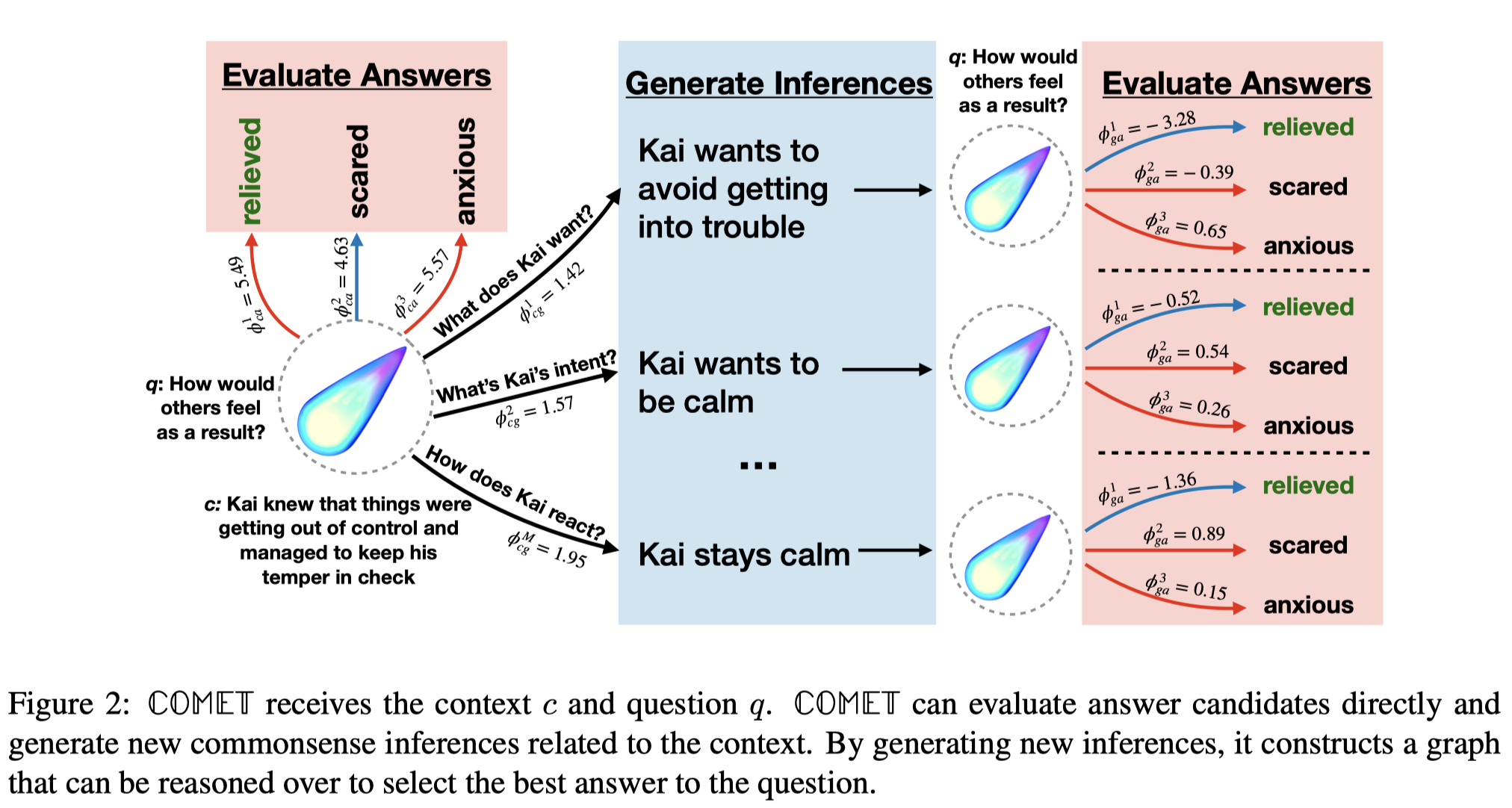
1. Building the Graph
生成 COMET 推理:
- COMET输入:context $c$ 和 ATOMIC relation type $r$;
- 输出:candidates $\mathcal{G}$, 每个 $g \in \mathcal{G}$ 的打分 $\phi_g$
- 计算:$\phi_g = \frac{1}{|g|}\sum_{s=1}^{|g|}log P(y_s | y_{<s}, c, r)$
- $y_s$ 是 $g$ 中的token;
- $|g|$ 是 长度;
- 每生成一个 $g$ 可以看成是基于 context 的 1-hop 推理;
- 根据 Markov 假设,将一步操作进行扩展,关于 context 的 l-hop 推理:
- $\phi_g^l = \phi_g^{l-1} + \frac{1}{|g^l|}\sum_{s=1}^{|g^l|}log P(y_s | y_{<s}, g^{l-1}, r)$
- 初始状态:
- $g^0 = c$, $\phi_g^0 = 0$
计算答案打分:
- 对于任意 $g\in \mathcal{G}$, 可以利用上述公式为每个后续答案计算一个分数:
- $\phi_a = \frac{1}{|a|}\sum_{t=1}^{|a|} log P(x_t | x_{<t}, q, g)$
- 对于每一个 $g \in \mathcal{G}^l$ , 都可以计算一个答案打分:
- $\phi_{ga}^l = \frac{1}{|\mathcal{G}^l|} \sum_{m=1}^{|\mathcal{G}^l|} \gamma_g \phi_g^{m,l} + \gamma_a \phi_a^{m,l}$
- $|\mathcal{G}^l|$ 是 l-hop 推理生成的推理数量
- 对于生成的 $g_m^l \in \mathcal{G}^l$
- $\phi_g^{m,l}$ 对应为路径打分;
- $\phi_a^{m,l}$ 对应为答案打分;
- $\gamma_g, \gamma_a$ 为超参数;
- $\phi_{ga}^l$ 可以看成是答案 $a$ 在推理路径 $\{c \rightarrow g^1 \rightarrow … \rightarrow g^l \}$ 下的打分;
- 定义基于生成推理的最大似然:
- (随着推理步数/推理层级 $L$ 的增加,生成的推理数量 $|\mathcal{G}^l|$ 也会增加,将很难为每个生成推理计算打分 $\phi_{ga}$ )
- $\phi_{ga_{max}}^l = max_{m\in [0,|\mathcal{G}^l|)} \gamma_g \phi_{g}^{m,l} + \gamma_a \phi_a^{m,l}$
- $[0,|\mathcal{G}^l|)$ 是所有可被索引的生成推理的范围;
2. Evaluating the Graph
Probabilistic Reasoning
- 当不同推理层级答案打分 $\{\phi_{ga}^l\}_0^L$ 计算出来后,可以通过计算边缘概率获得每个答案的最终打分,并选择得分最高的作为最终答案:
- $log P(a|q,c) \propto \phi_{ens} = \sum_{l=0}^L \beta_{ga}^l \phi_{ga}^l$
- $\hat{a} = argmax_{a\in \mathcal{A}} \phi_{ens}$
- $\beta_{ga}^l$ 是超参数,用于缩放每一hop的打分对最终的贡献;
- $\phi_{ga}^0$ 是直接利用context计算的答案打分;
Overcoming Answer Priors
- 考虑到某些候选答案在某些问题上出现的概率很高,而且与上下文无关;
- 利用PMI重新定义 $\phi_a$:
- $\phi_a \propto PMI(a,g|q)$
- $\phi_a = \frac{1}{|a|} \sum_{t=1}^{|a|} (log P(x_t | x_{<t},q,g) - log P(x_t | x_{<t}, q))$
Experiment
训练COMET: 使用 GPT2 (345M)作为 PLM 模型,解码策略默认为 argmax decoding;
超参数选择:
- $\gamma_g = \gamma_a = 1.0$
- 在 SocialIQA中: $\beta^l = 1.0$
- 在 Story Commonsense中: $\beta^l = 0.0$
实验结果与分析:参见论文
Summary & Analysis
- 1.COMET: Commonsense Transformers for Automatic Knowledge Graph Construction. ACL,2019. ↩