EMNLP2019 | What's Missing? A Knowledge Gap Guided Approach for Multi-hop Question Answering

Posted on | Post modified: | In | Post Total Visits
Words count in article: 2.6k | Reading time ≈ 11

Title: What’s Missing: A Knowledge Gap Guided Approach for Multi-hop Question Answering
Authors: Tushar Khot, Ashish Sabharwal, Peter Clark
Org.: Allen Institute for Artificial Intelligence
Published: EMNLP, 2019

Code: https://github.com/allenai/missing-fact

Motivation

大多数的RC任务/数据集假设给待测试系统（或模型）提供了回答问题所需要的所有知识。
实际上，在处理multi-hop类型的问题时，模型只能接触到部分的知识，那么想要正确地回答数据集中的问题，就必须基于问题和提供的知识，抽取出额外的知识/事实。
正是这部分额外的知识的存在，造成了 knowledge gap 问题。

本文对knowledge gap问题展开研究，目标是确定这样的 gap，并且利用额外的知识源填充这个 knowledge gap。

本文主要研究的数据集是 OpenBookQA[1]，可以看做是一类 提供了部分知识的QA任务。
OpenBookQA数据集的主要特点是：

  1. 问题的领域是科学事实
  2. 回答问题时，不仅需要从一个给定的 small book 中确定相关的核心科学事实（core science fact），还需要从外部的知识源中抽取出额外的常识知识。
    1. 这里的core fact就是数据集本身提供的partial knowledge
    2. 额外的外部知识 (broad external knowledge)，用以填充余下的 knowledge gap

OpenBookQA（OBQA） 中的 Knowledge Gap 示例：example

This Work

本文的主要工作：

  1. 在 OBQA 的基础上对 Knowledge Gap 进行了分析和标注，并发布了带标注的数据集；
  2. 提出了一个 two-step 方法，即先确定再填充（Knowledge Gap）的方法解决 Multi-hop QA 任务；
    1. 第一步，确定 knowledge gap：在 core fact 中预测一个 key span；
      • 这一步实际上是阅读理解中 span extraction 类型任务，本文中使用了 BIDAF 模型；
    2. 第二步，填充 knowledge gap：确定 key span 和候选项之间的关系，然后回答问题；
      • 具体分为3个子步骤：(a) 从 ConceptNet/text corpora[2] 中抽取相关知识；(b) 预测 key span 和 候选答案之间的潜在关系；(c) 组合 core fact 和 抽取的外部知识来填充gap；
      • 这一步中，采取multi-task学习，联合学习 gap 的关系预测 和 最终的答案预测；
  3. 提出了一个模型，同时学习使用抽取得到的 external knowledge，并与 partial knowledge 组合来填充 knowledge gap；

Knowledge Gaps

Understanding Gaps

针对 OBQA 任务，可以将 Knowledge Gap 分为三类（见下面的 Figure-2），这种分类也适用于其他的multi-hop QA数据集。

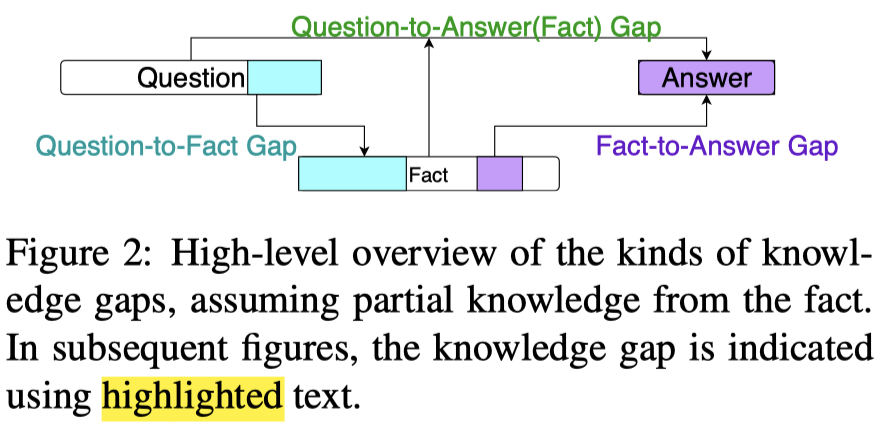
  • gap-class-all
  • 注：OBQA中的核心组成部分：数据集中显示给出的1、Question；2、Answer Choices；3、Fact；以及未在数据集中出现但是对回答问题重要的4、external knowledge；

Question-to-Fact : 存在于问题中的概念（concept）和 core fact 之间；

  • 例如: gap-1

Fact-to-Answer : Gap 捕捉的是 core fact 中的概念和候选答案之间的关系；

  • 例如: gap-2
  • fact 中的概念可能和不正确的选项之间也存在关系

Question-to-Answer (Fact) : 基于 core fact，问题中的概念和候选答案需要额外的知识（gap）来建立联系；

  • 例如: gap-3

根据抽样统计，在OBQA中 Q2F（44%） 和 F2A（86%） 这两种Gap比较常见，Q2A（<20%） 类型比较罕见，一些问题可能存在多种gaps。

本文只关注 Fact-to-Answer gap，并且假设所需的 core fact 已经给定。

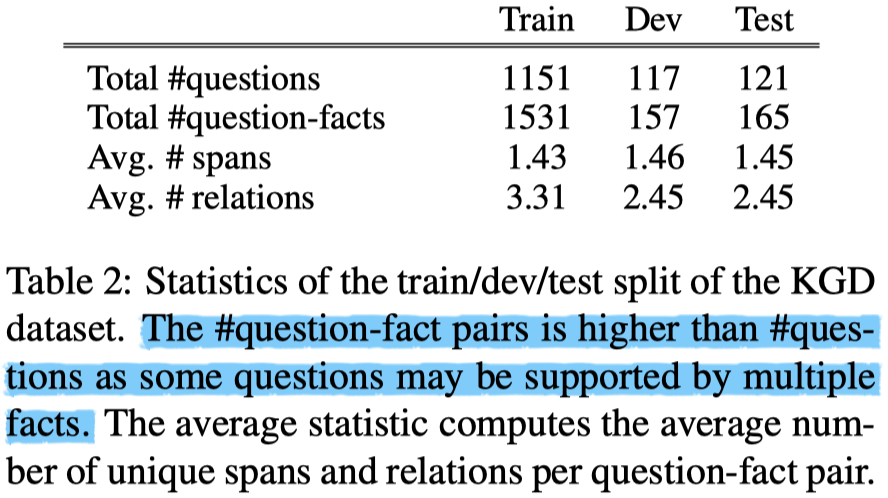
Knowledge Gap Dataset: KGD

（文章中介绍了采取众包对数据集中每个样例的knowledge gap进行标注的细节，具体细节请参考文章的 Section 3.2 以及 Appendix A。这里直接介绍标注得到的数据集KGD）

在KGD中，包含了 Key Span 和 relation label 的标注，用以表示knowledge gap。

  • span 是 fact 的子串，relations 是 span 和正确答案之间的关系集合
  • KGD示例：kgd
  • KGD数据统计：kgd-s

Knowledge-Gap Guided QA: GapQA

模型介绍中涉及的符合及其含义：

  • question $q$；fact $f$；selected span $s$；set of relations between span and correct choice $r$；answer choices $c$；question stem $q_s$
    • 其中：$q=q_s c$
  • tokens in question stem $q_m$；tokens in fact $f_m$；
  • predicted span $\hat{s}$；predicted relations $\hat{r}$

1.Key Span Identification Model

模型采用 BIDAF；
训练时，模型的输入为：fact（对应于passage），question stem（对应于question），模型的输出是 key span 的起止位置；

2.Knowledge Retrieval Module

给定一个预测的span，从两个知识源中抽取知识，用 $K$ 表示所有抽取到的知识：

  1. ConceptNet 中的三元组，三元组中的relation与gap需要的relation密切相关；
  2. ARC corpus 中的句子，ARC corpus 包含 14M 科学相关的句子，用来补充 CN，提高recall；

Tuple Search：

  1. 选择tuple时，要求subject中至少有一个token 与 $\hat{s}$ 匹配，object中至少有一个词与 $c_i$ 匹配（反之亦然）；
  2. 通过 Jaccard score 对于tuples进行打分，为每个候选选项 $c_i$ 选择出 top-k 个 tuples（在实验中，k=5）
    • $\text{Jaccard score}(t) = \text{jacc}(\text{tokens}(t), \text{tokens}(\hat{s} + c_i))$
    • $\text{jacc}(w_1, w_2) = \frac{w_1 \cap w_2}{w_1 \cup w_2}$
  3. 为了知识形式的一致性，将三元组也转化为句子的形式；

Text Search：

  1. 使用 ElasticSearch 进行相关句子的检索，查询为：$\hat{s} + c_i$：
  2. 为每个候选选项 $c_i$ 选择出 top-5 个句子

3.Question Answering Module

模型结构图: 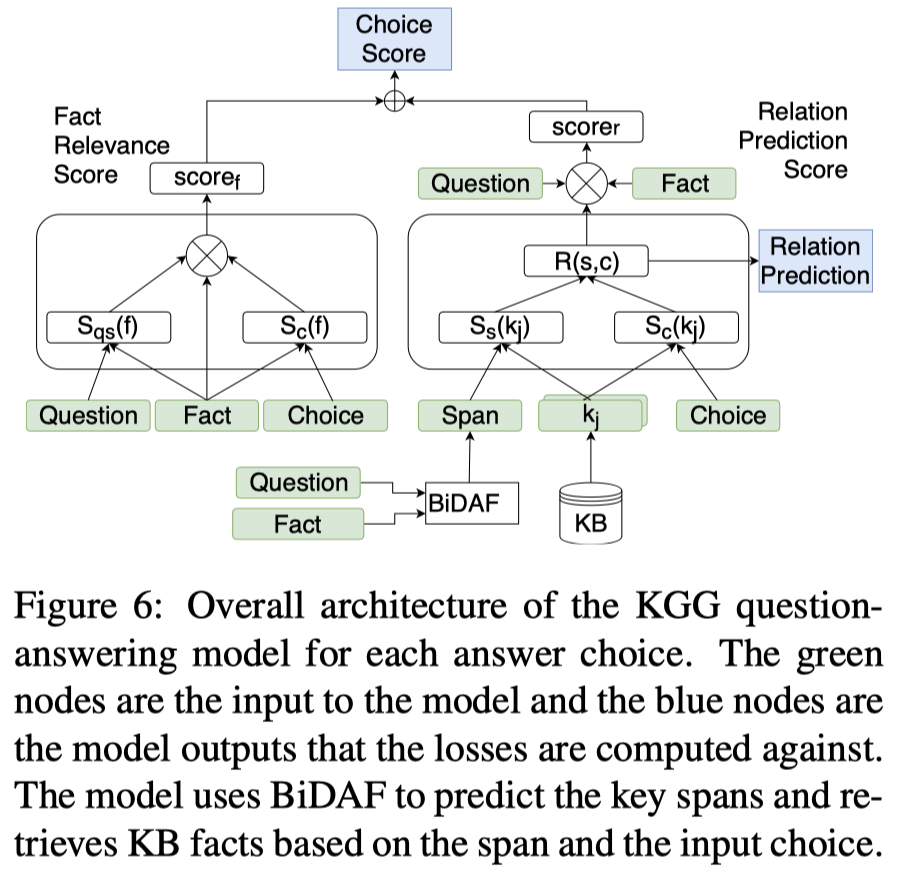kgg-qa-module

本模块的输入为：$q_s$, $c$, $f$, $\hat{s}$, $K$；

计算过程如下：

Step 1. Embedding: 使用 300维 的glove 词向量表示输入中的每个词

Step 2. Encoding: 使用 BiLSTM 计算上下文编码，隐藏层维度为100，用 $\mathcal{E}_*$ 表示 BiLSTM 的输出

Step 3. Fact Relevance:

出发点：一个相关 fact 可以捕捉到与问题和正确答案对齐的概念间的关系；

  1. 计算 question-weighted 和 answer-weighted fact表示；
    • question-weighted fact repr.
      • $\mathcal{A}_{q_s,f} = \mathcal{E}_{q_s} \cdot \mathcal{E}_f \in \mathbb{R}^{q_m \times f_m}$
      • $\mathcal{V}_{q_s}(f) = \text{softmax}_{f_m}(\text{max}_{q_m} \mathcal{A}_{q_s,f}) \in \mathbb{R}^{1 \times f_m} $
      • $\mathcal{S}_{q_s}(f) = \mathcal{V}_{q_s}(f) \cdot \mathcal{E}_f \in \mathbb{R}^{1 \times h}$
    • choice-weighted fact repr. $\mathcal{S}_{c_i}(f)$
      • 同样的计算方式，将 $q_s$ 的表示替换为 $c_i$
  2. 组合计算的 fact-based 表示，确定 fact 对 choice 的支持程度；
    • 组合两种 fact 表示：$\mathcal{S}_{q_s c_i}(f) = (\mathcal{S}_{q_s}(f) + \mathcal{S}_{c_i}(f))/2$
    • 计算候选答案的打分:
      • $\text{score}_f(c_i) = \text{FF}(\bigotimes( \mathcal{S}_{q_s c_i}(f) , \text{avg} \mathcal{E}_f))$
      • $\bigotimes(x,y) = [x-y; x \ast y] \in \mathbb{R}^{1 \times 2h}$
      • $\text{FF}$ 是 前馈神经网络，输出一个标量值；

Step 4. Filling the Gap:

实现上是预测 $\hat{s}$ 和 $c_i$ 之间的关系，并将关系和fact进行组合，为choice进行打分

  1. 计算 span weighted 和 choice weighted KB知识句表示 ($\in \mathbb{R}^{1 \times h}$)，反映知识句中的词分别和 span 以及 choice 的相关程度
    • $\mathcal{S}_{\hat{s}}(k_j) = \mathcal{V}_{\hat{s}}(k_j) \cdot \mathcal{E}_{k_j}$
    • $\mathcal{S}_{c_i}(k_j) = \mathcal{V}_{c_i}(k_j) \cdot \mathcal{E}_{k_j}$
  2. kb-based relation repr.：
    • $\mathcal{R}_j (\hat{s}, c_i) = \text{FF}(\bigotimes(\mathcal{S}_{\hat{s}}(k_j), \mathcal{S}_{c_i}(k_j)) ) \in \mathbb{R}^{1 \times h}$
  3. 聚集所有KB知识句的relation repr.:
    • $\mathcal{R}(\hat{s}, c_i) = \text{avg}_j \mathcal{R}_j (\hat{s}, c_i)$

Step 5. Relation Prediction Score:

  1. 基于问题，确定/预测与fact信息相符合的relation信息 (通过聚集问题和fact的表示来捕获这个信息)
    • $\mathcal{D}(q_s, f) = \bigotimes(\text{max}_{q_m} \mathcal{E}_{q_s}, \text{max}_{f_m} \mathcal{E}_{f}) \in \mathbb{R}^{1 \times 2h}$
  2. 基于fact信息和relation表示，对每个候选项进行打分
    • $\text{score}_r(c_i) = \text{FF}([\mathcal{D}(q_s, f); \mathcal{R}(\hat{s}, c_i)])$

Step 6. Final score for each choice: $\text{score}(c_i) = \text{score}_f(c_i) + \text{score}_r(c_i)$

4. Model Training

GapQA 中 Question Answering Module 的总训练 loss 由两部分组成：

  1. 模型预测的答案和正确的答案选项之间的交叉熵损失
  2. 模型预测的relation（span 和 候选项之间）与正确relation之间的损失：
    • 为了计算这部分的损失，使 $\mathcal{R}(s,c_i)$ 通过一层的ffn，映射为向量 $\hat{r}_i \in \mathbb{R}^{1\times l}$，$l$ 是 relation 的个数；
    • 由于$(s,c_i)$对之间可能存在多个有效的relation，创建一个 n-hot 向量表示 $\bar{r} \in \mathbb{R}^{1\times l}$，如果 relation $r_k$ 是有效的，则令 $\bar{r}[k] = 1$；
    • 对于正确的选项（即问题的目标答案），使用 binary cross-entropy 计算预测的 $\hat{r}_i$ 和 $r$ 之间的损失；
    • 对于不正确的选项，无法确定 span 和选项之间的relation关系（不存在标注信息），但是针对正确答案选择出的 relations set 不应对错误选项有效。故此，使用 binary cross-entropy 计算预测的 $\hat{r}_i$ 和 $1-r$ 之间的损失，并且不考虑未被选中的 relation，即使用 masked binary cross-entropy；
    • （这里选中的 relations 指的是：KGD中对 key span 和 correct choice 之间标注的relation集合）

最终，总体的 $loss = ce(\hat{c}, \bar{c}) + \lambda \cdot (bce(\hat{r}_i, \bar{r}) + \sum_{j\neq i} mbec(\hat{r}_j, 1-\bar{r}, \bar{r}) )$

为了更清晰的理解模型的整体计算流程，附录中给出了一个可视化的示例：eg-vis

Experiments

  1. Key Span Identification 效果：exp-span
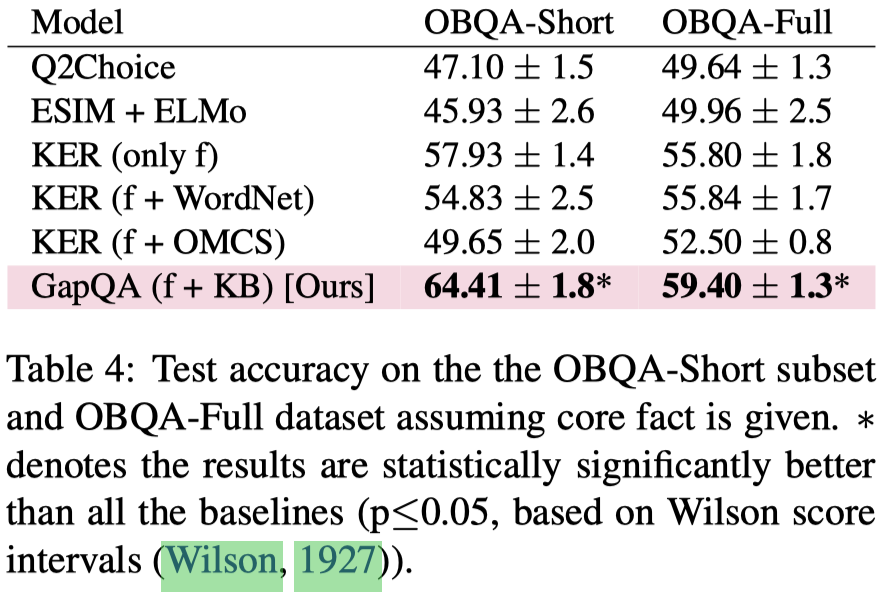
  2. 在 OBQA 数据集上的结果：exp-main
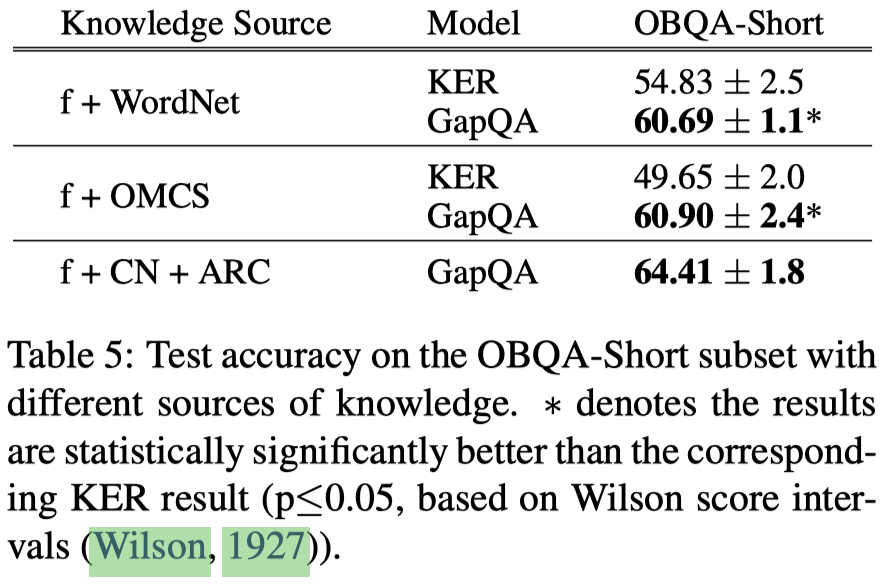
  3. 输入知识源的影响：exp-k
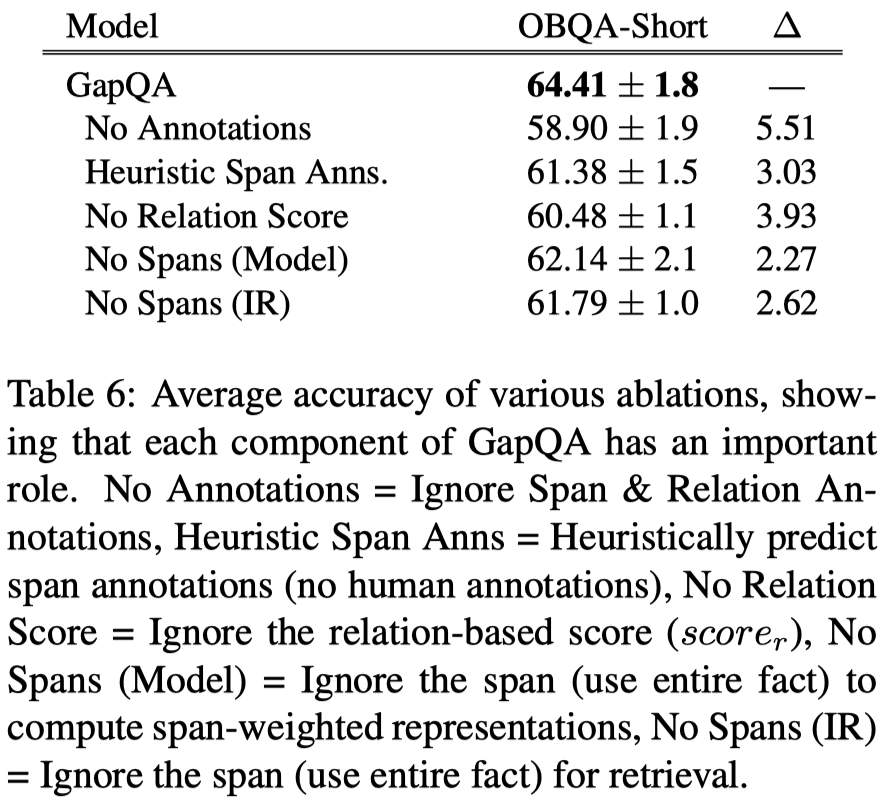
  4. 模型去除实验：exp-a
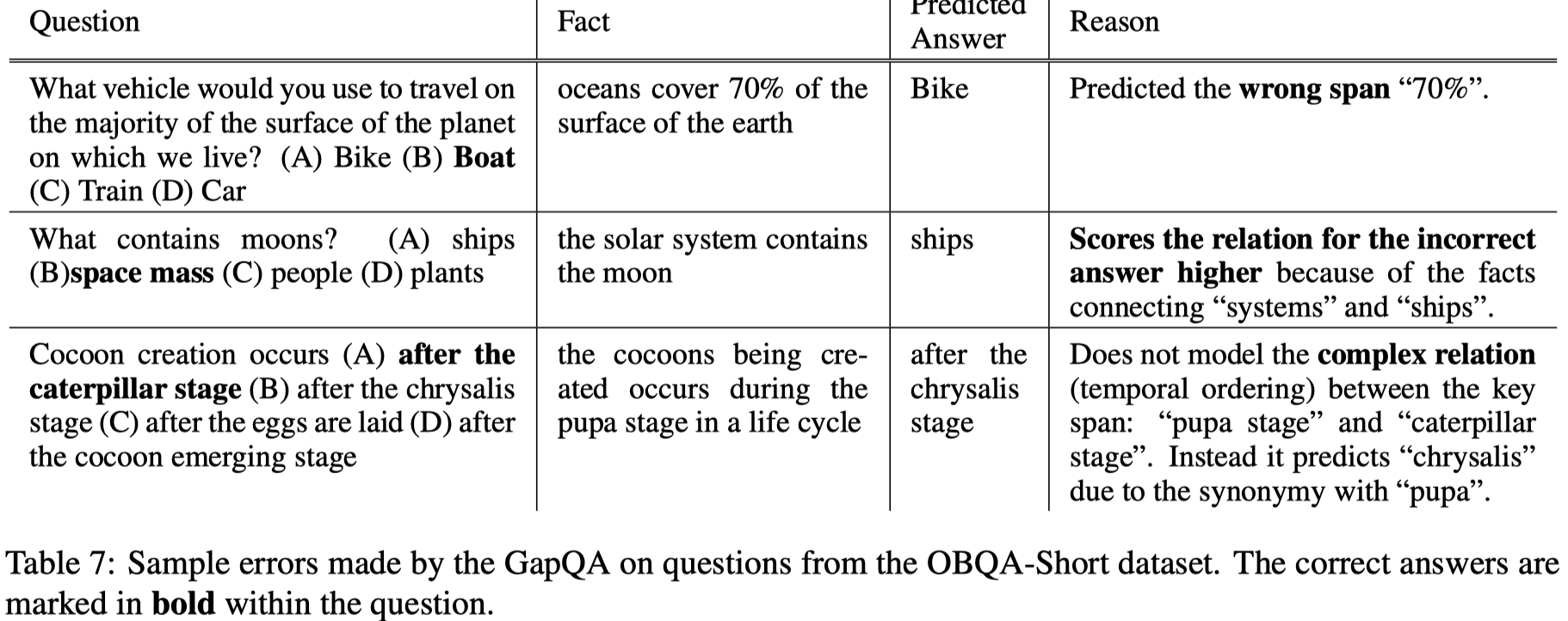
  5. 错例分析：exp-error

主要存在三种错误类型：
(1) Incorrect predicted spans (25%)
(2) Incorrect relation scores (55%)
(3) Out-of-Scope Gap relations (20%)

Analysis & Summary

  • 这篇文章，对于 OBQA 类 partial knowledge multi-hop QA 的任务，引入了一个新颖的问题定义，旨在刻画QA任务中知识缺失的本质问题，并对这个问题进行了细致化的分类。不仅给出了可引入监督信息的标注过程和相应的数据集，同时也提出了有说服力的模型；

  • 本文中只对最常见的 Fact-to-Answer Gap 问题进行了研究，针对其余两种 knowledge gap 的解决方案同样值得后续的研究；

    • 针对MCQ类任务，才会存在涉及到 Answer 的 Gap，那么如果在任务中未给出候选答案的情况下，

  • 从解决方法上看，先确定在填充整体上为pipline的形式，在实验部分没有看到使用标注的gold span进行GapQA计算的结果？

  1. 1.Can a suit of armor conduct electricity? A new dataset for open book question answering. 2018. Todor Mihaylov, Peter Clark, Tushar Khot, and Ashish Sabharwal. In EMNLP. ↩
  2. 2.Think you have solved question answering? Try ARC, the AI2 reasoning challenge. 2018. Peter Clark, Isaac Cowhey, Oren Etzioni, Tushar Khot, Ashish Sabharwal, Carissa Schoenick, and Oyvind Tafjord. CoRR, abs/1803.05457. ↩
**** END of This Post. Thank for Your READING ****
If you have any Question, welcome to Email me or leave your comments below.