Title: Modeling Semantic Compositionality with Sememe Knowledge
Authors: Fanchao Qi, Junjie Huang, Chenghao Yang, Zhiyuan Liu, Xiao Chen, Qun Liu, Maosong Sun
Org: Tsinghua University, Beihang University, Huawei Noah’s Ark Lab
Published: ACL 2018
official code: https://github.com/thunlp/Sememe-SC
Task Definition
- Semantic Compositionality (SC, 语义组合):
- is defined as the linguistic phenomenon that the meaning of a syntactically complex unit is a function of meanings of the complex unit’s constituents and their combination rule [1]
- Multiword Expressions (MWE, 多字/词表达):
- 大多数关于 SC 的工作都是集中在 基于向量的分布式语义模型来学习 多字/词构成的 短语、成分的表示
- 基本框架(公式1),以两个词为例:
- 其中:
- $f$ 是组合函数
- $\mathbf{p}$ 是MWE的embedding
- $\mathbf{w}_1$ 和 $\mathbf{w}_2$ 表示 MWE 成分的embedding,也就是 组成 MWE 的词的表示
- $R$ 是 组合规则(Combination Rule)
- $K$ 指在构建MWE语义时需要的额外的知识
- 其中:
- Sememe (义原):
- the minimum Semantic units of human language
- all the words can be composed of a limited set of sememes, which is similar to the idea of semantic primes (语义启动)[2]
- HowNet:义原知识库
Motivation
- 之前的工作:利用复杂的组合函数,而很少考虑外部知识
This Work
- 1、设计了一个简单的 Semantic Compositionality Degree (SCD,语义组合程度) 测量实验:
- 通过实验发现 MWE 的 SCD 可以通过简单的基于义原的公式计算,并且和人类的判断高度相关
- 义原可以很好的刻画 MWE 的含义和 MWE 的组成成分,并且可以捕捉这两者之间的语义关联
- 证实:义原适用于建模 SC,并且可以提高 SC 相关任务的效果,如 MWE 表示学习
- 2、提出了两个结合义原的SC模型同于学习 MWE embedding,同时将公式1中的组合规则也结合到了两个模型中:
- 模型1:Semantic Compositionality with Aggregated Sememe model (SCAS)
- 模型2:Semantic Compositionality with Mutual Sememe Attention model (SCMSA)
- Note: 在这篇文章中,主要关注两个词组成的中文 MWE 的语义组合建模
Measuring SC Degree with Sememes
这一部分的主要工作是通过一个SCD验证实验来证明义原适用于建模语义组合
Sememe-based SCD Computation Formulae
基于义原的SCD计算规则
基本原则:
- 不同的MWE具有不同的 SC degrees
- 一个词的所有义原可以准确的描述一个词的意思
启发式的设计了SCD的计算规则集合,见下图:

- 数字越大表示SCD值越高
- $S_p$, $S_{w_1}$, $S_{w_2}$ 分别表示 MWE 的义原集合 和 MWE 两个组成成分(词)的义原集合
- SCD = 3:
- MWE 的义原集合为两个组成成分义原集合的的并集(union)相同
- 也就是说,MWE 的含义正好是两个成分含义的组合
- the MWE is fully semantically compositional
- SCD = 2:
- MWE 的义原集合为两个组成成分义原集合的的并集(union)的一个适合的子集
- 组成成分的语义有覆盖 MWE 语义的部分,但是不能准确的推出 MWE 的语义
- SCD = 1:
- MWE 与 组成成分共享一部分义原,但是他们分别具有各自私有的义原
- SCD = 0:
- MWE 的含义与其组成成分的含义完全不同
- 无法从组成成分的含义中推出 MWE 的语义
- the MWE is completely non-compositional
Evaluation
构建了一个人工标注的SCD数据集
评测人工标注的与规则预测的SCD之间的相关系数 (Pearson 和 Spearman)
Sememe-incorporated SC Models
Incorporating Sememes Only
仅结合义原计算 MWE 的情况对应于公式1的一个简化:
- $\mathbf{p} = f(w_1, w_2, K)$
- 使用 $S$ 表示所有的义原集合,词w的义原集合为 $S_w = \{s_1, …, s_{|S_w|}\} \subset S$
- $w$ 和 $\mathbf{s}$ 的 embedding 维度都是 $\mathbb{R}^d$
Semantic Compositionality with Aggregated Sememe model (SCAS)
SCAS 的结构如下图所示:
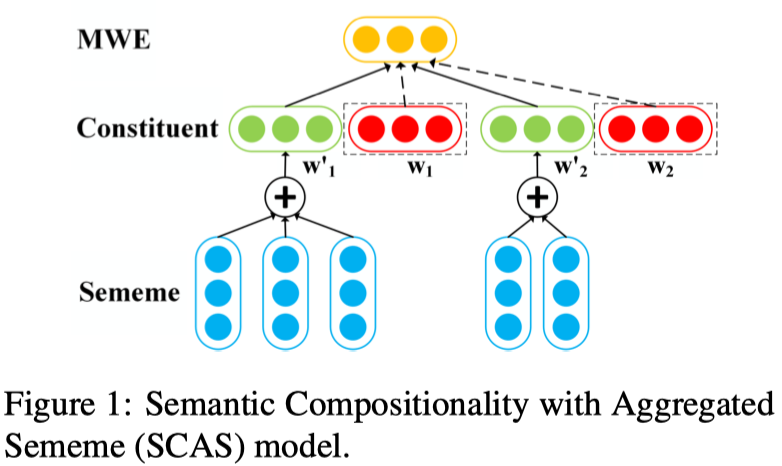
- SCAS 模型仅仅串联了MWE组成成分和他们的义原的embedding
- $\mathbf{p} = \text{tanh} (W_c [w_1 + w_2; w_1^\prime + w_2^\prime] + b_c)$
- $w_1^\prime = \sum_{s_i \in S_{w_1}} \mathbf{s}_i$
- $w_2^\prime = \sum_{s_j \in S_{w_2}} \mathbf{s}_j$
Semantic Compositionality with Mutual Sememe Attention model (SCMSA)
SCMSA 的结构如下图所示:
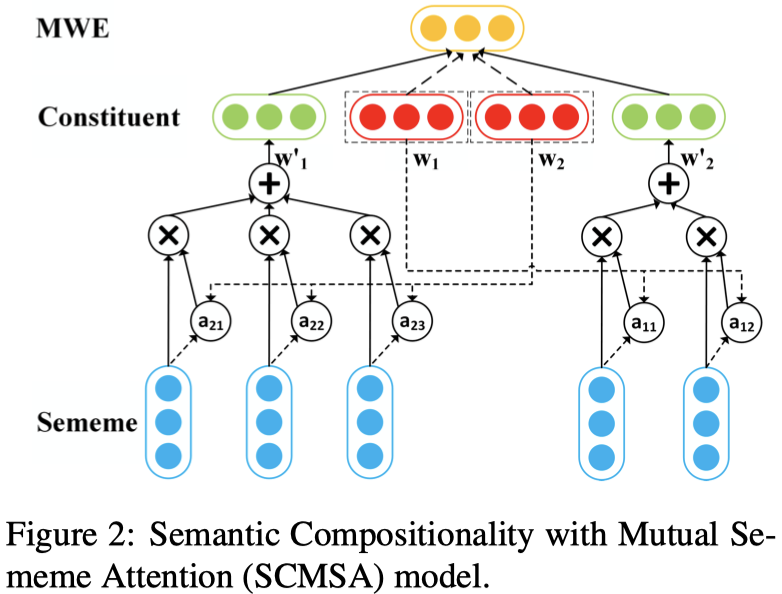
- SCMSA 模型 计算了 一个组成成分的义原的 Mutual Attention 以及 与其他成分的义原集合的 Mutual Attention
- 动机:组成成分之间的义原互不相同,在进行义原组合的时候,MWE 的义原应对组成成分的义原应该分配不同的权重
- $\mathbf{p}$ 的计算与SCAS相同,不同的是 $w^\prime$的计算:
- $\mathbf{e}_1 = \text{tanh} (W_a w_1 +b_a)$
- $a_{2,i} = \frac{\text{exp}(\mathbf{s}_i \cdot \mathbf{e}_1)}{\sum_{s_j \in S_{w_2}} \text{exp}(\mathbf{s}_j \cdot \mathbf{e}_1) }$
- $w_2^\prime = \sum_{s_i \in S_{w_2}} a_{2,i} \mathbf{s}_i$
Integrating Combination Rules
根据原始的公式1:
- 使用不同的MWE组合矩阵来表示不同的组合规则,即:
- $W_c = W_c^r, r\in R_s$
- $W_c^r \in \mathbb{R}^{d \times 2d}$
- $R_s$ refers to combination rule set containing syntax rules of MWE
- e.g., adjective-noun, noun-noun
- $W_c = W_c^r, r\in R_s$
- 考虑到组合矩阵的稀疏性,以及组合矩阵之间会存在通用的组合信息,将上述矩阵进行拆分:
- $W_c = U^rV^r + W_c^c$
- $U^r \in \mathbb{R}^{d \times h_r}$
- $V^r \in \mathbb{R}^{d \times h_r}$
- $h_r \in \mathbb{N}_+$ 为超参数,根据组合规则变化
- $W_c^c \in \mathbb{R}^{d\times 2d}$
- $W_c = U^rV^r + W_c^c$
Training Objective
training for MWE similarity computation
- squared Euclidean distance
training for MWE sememe prediction
- weighted cross-entropy loss